在数学中,数?x(对于底数?β)的对数是βy?的指数?y,使得?x=βy。底数?β?的值一定不能是1或0(在扩展到复数的复对数情况下不能是1的方根),典型的是e、?10或2。数x(对于底数β)的对数通常写为
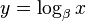 。
。当x和β进一步限制为正实数的时候,对数是1个唯一的实数。 例如,因为
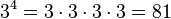 ,
,我们可以得出
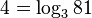 ,
,用日常语言说,对81以3为基的对数是4。
目录[隐藏] |
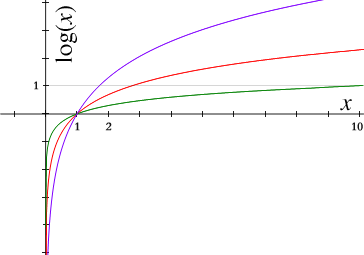
函数logαx依赖于α和x二者,但是术语对数函数在标准用法中用来称呼形如logαx的函数,在其中底数α是固定的而只有一个参数x。所以对每个基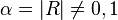 的值(不得是负数、0或1)只有唯一的对数函数。从这个角度看,底数α的对数函数是指数函数y = αx的反函数。词语“对数”经常用来称呼对数函数自身和这个函数的1个特定值。
的值(不得是负数、0或1)只有唯一的对数函数。从这个角度看,底数α的对数函数是指数函数y = αx的反函数。词语“对数”经常用来称呼对数函数自身和这个函数的1个特定值。
对数函数图像和指数函数图像关于直线y=x对称,互为逆函数。
对数函数的性质有:
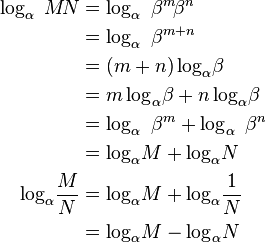

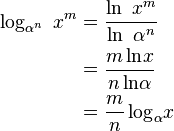
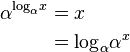
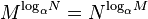


 。
。但是,如果β是不等于1的正实数,这个定义可以扩展到在一个域中的任何实数n(参见幂)。类似的,对数函数可以定义于任何正实数。对于不等于1的每个正底数β,有一个对数函数和一个指数函数,它们互为反函数。
对数可以简化乘法运算为加法,除法为减法,幂运算为乘法,根运算为除法。所以,在发明电子计算机之前,对数对进行冗长的数值运算是很有用的,它们广泛的用于天文、工程、航海和测绘等领域中。它们有重要的数学性质而在今天仍在广泛使用中。
最常用做底数的是e 、10和2。当写出不带底数的“log”的时候,意图要从上下文中确定:
、10和2。当写出不带底数的“log”的时候,意图要从上下文中确定:
 ,有时写为
,有时写为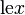 );在微积分、数论中。
);在微积分、数论中。 或简写(极易产生歧义)为
或简写(极易产生歧义)为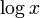 ,有时写为
,有时写为 ;在工程中和在使用对数表简化计算的时候。
;在工程中和在使用对数表简化计算的时候。 ;有时写为lbx;在信息论和音程中。
;有时写为lbx;在信息论和音程中。为了避免混淆,在可能有歧义的时候最好指定底数。
尽管有很多有用的恒等式,对计算器最重要的是找到不是建造于计算器内的底数(通常是loge和log10)的其他底数的对数。要使用其他底数β找到底数α的对数:
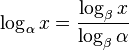 。
。此外,这个结果蕴涵了所有对数函数(任意底数)都是相互类似的。所以用计算器计算对1344217728底数2的对数:
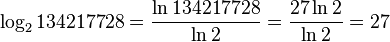 。
。对数对解幂是未知的方程是有用的。它们有简单的导数,所以它们经常用在解积分中。对数是三个相关的函数中的一个。在等式bn = x中,b可以从x的n次方根,n从x 的b底数的对数,x从b的n次的幂来确定。参见对数恒等式得到掌控对数函数的一些规则。
对数把注意力从平常的数转移到了幂。只要使用相同的底数,就会使特定运算更容易:
| 数的运算 | 幂的运算 | 对数恒等式 |
|---|---|---|
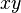 | 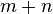 |  |
 | 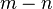 | 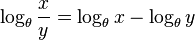 |
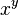 |  |  |
![\sqrt[y]{x}](http://upload.wikimedia.org/math/8/9/b/89b0836496d5a0309973d558fd8bd48c.png) |  | ![\log_{\theta}\sqrt[y]{x}=\frac{\log_{\theta}x}{y}](http://upload.wikimedia.org/math/d/c/5/dc5eaab05c0c70592f5486f6514e25d3.png) |
这些关系使在两个数上的这种运算更快,在乘法计算器出现之前正确的使用对数是基本技能。
从纯数学的观点来看,恒等式
 ,
,在两种意义上是基本的。首先,其他3个算术性质可以从它得出。进一步的,它表达了在正实数的乘法群和所有实数的加法群之间的同构。
对数函数是从正实数的乘法群到实数的加法群的唯一连续同构。
复对数计算公式
![{}_{{\color{blue}{\rm{Log}}_{c+d{\rm{i}}} (a+b{\rm{i}}) =\frac{\ln\left(a^2+b^2)\cdot\ln(c^2+d^2\right)+4\left(\arctan\frac{a}{b}+2k\pi\right) \left(\arctan\frac{d}{c}+2n\pi\right) +\left[2\left(\arctan\frac{b}{a}+2k\pi\right)\ln\left(c^2+d^2\right)-2\left(\arctan\frac{d}{c}+2n\pi\right)\ln\left(a^2+b^2\right)\right]{\rm{i}}}{\ln^2\left(c^2+d^2\right)+4\left(\arctan\frac{d}{c}+2n\pi\right)^2}}}](http://upload.wikimedia.org/math/6/5/a/65ab7405859fadde284b16583f2b262d.png) ,
,![{}_{{\color{red}\ (a+b{\rm{i}})^{\left(c+d{\rm{i}}\right)}=e^{\frac{c}{2}\ln\left(a^2+b^2\right)-\left(d+2n\pi\right)\left(\arctan\frac{b}{a}+2k\pi\right)}\left\{\cos \left[c\left(\arctan\frac{b}{a}+2k\pi\right)+\frac{1}{2}\left(d+2n\pi\right)\ln\left(a^2+b^2\right)\right] +{\rm{i}}\sin\left[c\left(\arctan\frac{b}{a}+2k\pi\right)+\frac{1}{2}\left(d+2n\pi\right)\ln\left(a^2+b^2\right)\right]\right\}}}](http://upload.wikimedia.org/math/0/6/2/0621f3243ab46e571c7b484395233a45.png)
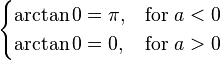

自然对数函数的导数是
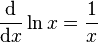 。
。通过应用换底规则,其他底数的导数是
 。
。自然对数 的不定积分是
的不定积分是
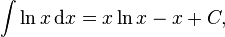
而其他底数对数的不定积分是
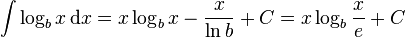 。
。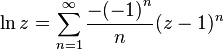 当
当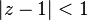 。
。下做推导:
由
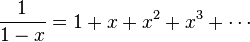 。
。在两边积分得到
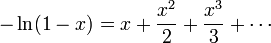
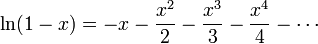 。
。设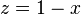 并因此
并因此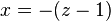 ,得到
,得到
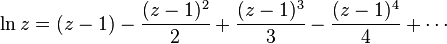
更有效率的级数是
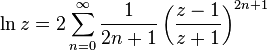
对带有正实部的z。
推导:代换-x为x,得到
 。
。做减法,得到
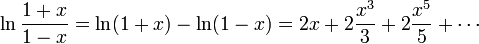 。
。设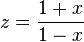 并因此
并因此 ,得到
,得到
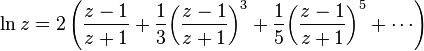 。
。例如,应用这个级数于
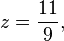
得到

并因此
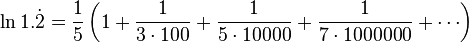

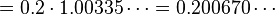
在这里我们在第一行的总和中提出了因数1/10。
对于任何其他底数β,我们使用
 。
。多数计算机语言把log(x)用做自然对数,而常用对数典型的指示为log10(x)。参数和返回值典型的是浮点数据类型。
因为参数是浮点数,可以有用的做如下考虑:
浮点数值x被表示为尾数m和指数n所形成的
因此
所以,替代计算ln(x),我们计算对某个m的ln(m)使得1 ≤ m ≤ 2。有在这个范围内的m意味着值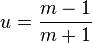 总是在范围
总是在范围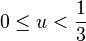 内。某些机器使用在范围
内。某些机器使用在范围 内的尾数,并且在这个情况下u的值将在范围
内的尾数,并且在这个情况下u的值将在范围 内。在任何一种情况下,这个级数都是更容易计算的。
内。在任何一种情况下,这个级数都是更容易计算的。
普通的正实数的对数一般化为负数和复数参数,尽管它是多值函数,需要终止在分支点0上的分支切割,来制作一个普通函数或主分支。复数z的(底数e)的对数是复数ln(|z|) + i arg(z),这里的 |z| 是z的模,arg(z)是辐角,而i是虚单位;详情参见复对数。
离散对数是在有限群理论中的相关概念。它涉及到解方程bn = x,这里的b和x是这个群的元素,而n是指定在群运算上的幂。对于某些有限群,据信离散对数是非常难计算的,而离散指数非常容易。这种不对称性可用于公开密钥加密。
对于不等于1的每个正数b,函数logb (x)是从在乘法下的正实数的群到在加法下(所有)实数的群的同构。它们是唯一的连续的这种同构。对数函数可以扩展为在乘法下正实数的拓扑空间的哈尔测度。
评论